SALA VIRTUAL 9º ANO

Olá Turma!

Explicação (Professor Eduardo)

Equações biquadradas é uma equação escrita da seguinte forma geral: ax⁴ + bx² + c = 0. Para resolver (encontrarmos as sua raízes) é preciso transformá-las em uma equação do segundo grau.

Para melhor compreensão veja no exemplo abaixo como essa transformação acontece e como chegamos às raízes da equação biquadrada.

y⁴ – 10y² + 9 = 0 → equação biquadrada

(y²)² – 10y² + 9 = 0 → também pode ser escrita assim.

Substituindo variáveis: y² = x, isso significa que onde for y² iremos colocar x.

x² – 10x + 9 = 0 → agora resolvemos essa equação do 2º grau encontrando x` e x``

a = 1    b = -10     c = 9

∆ = b² – 4ac
∆ = (-10)² – 4 . 1 . 9
∆ = 100 – 36
∆ = 64

x = - b ± √∆ 
            2a

x = -(-10) ± √64
             2 . 1

x = 10 ± 8
           2

x’ = 9

x” = 1

Essas são as raízes da equação x² – 10x + 9 = 0, para encontrarmos as raízes da equação biquadrada y⁴ – 10y2 + 9 = 0 devemos substituir os valores de x’ e x” em y² = x.

Para x = 9
y² = x
y² = 9
y = ± √9
y = ± 3

Para x = 1
y² = x
y² = 1
y = ± √1
y = ±1

Portanto, a solução da equação biquadrada será:

S = {-3, -1, 1, 3}.

Ok! acredito que ficou bem exlicado.

Agora é com vocês. 

Copiar no caderno e resolver. (Será solicitado caderno e chamada ao quadro para se obter a nota máxima).

Determine o conjunto solução da seguinte equação biquadrada: x⁴ – 5x² + 4 = 0.

Calcule as raízes da seguinte equação: 4x⁴ – 9x² + 2 = 0. 

Calcule as raízes da seguinte equação x⁶ + 117x³ – 1000 = 0. (Essa eu vou iniciar).

Vejam que (x³)² é igual a x elevado a sexta. = 

Logo Y=X³ ok! o resto da solução é igual ao já estudado.

Resolva a equação 3x² * (x² – 5) = 5 – x².

Geometria

O teorema de Pitágoras relaciona as medidas dos lados de um triângulo retângulo da seguinte maneira:

Em um triângulo retângulo o quadrado da hipotenusa é igual à soma dos quadrados dos catetos. 

O teorema de Pitágoras é muito importante para aMatemática, tendo influenciado outros grandes resultados matemáticos. Veja também uma das demonstrações do teorema e parte da biografia de seu criador.

Fórmula:

Para aplicação do teorema de Pitágoras, é necessário compreender as nomenclaturas dos lados de um triângulo retângulo. O maior lado do triângulo fica sempre oposto ao maior ângulo que é o ângulo de 90°. Esse lado recebe o nome de hipotenusa e será representado aqui pela letra a.

Os demais lados do triângulo são chamados de catetos e serão aqui representados pelas letras b e c.

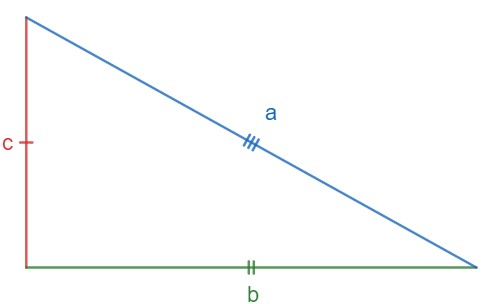
O teorema de Pitágoras afirma que é válida a relação a seguir:

Assim, podemos dizer que o quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos.

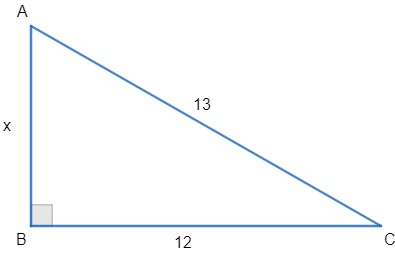
Determine o valor de x no triângulo a seguir.

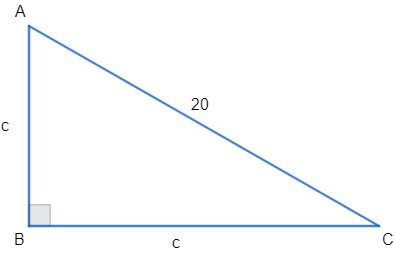
Determine a medida c dos catetos de um triângulo retângulo isósceles em que a hipotenusa mede 20 cm.

Na figura acima, que representa o projeto de uma escada com 5 degraus de mesma altura, o comprimento total do corrimão é igual a:

Otimo Estudota